(TF)² #5 – Vad händer när en AI tvekar?
Ibland trycker man bara in all sin data i en modell, får ett svar och så är man nöjd. Men så ser vår vardag nästan aldrig ut. Vi måste veta hur modellen ska användas. Hur ska beslut fattas ovanpå vårt svar?
Låt oss säga att du äger ett åkeri. Ni kör lastbils-leveranser på flera platser runt om i världen och är glada och stolta över detta. Ett stort inkomstbortfall kommer dock när lastbilarna går sönder, så du kommer till oss på Tenfifty och frågar “Kan ni hjälpa oss att förutsäga när lastbilarna kommer gå sönder?”. “Javisst, det kallas predictive maintenance” säger vi och frågar vad du har för data. Du berättar då att du tror att lastbilar har större risk att gå sönder tidigt ju ryckigare förarna kör, så du har samlat en stor databas med hur mycket varje lastbil har accelererat och bromsat varje dag, samt när de har gått sönder.
Vi skrider till verket och kommer tillbaka med en modell där du kan skicka in medel-ryckighet och miltal på en lastbil och så ger vi tillbaka hur många mil lastbilen har kvar. Vi berättar att våra körningar säger att den i snitt har 20% fel, något vi kallar MAE eller absolut medelfel. Nu har du en modell och vet hur osäker den är. Slutet gott allting gott? Nja.
Osäkerhet
Om du ska ta viktiga beslut baserat på vad modellen säger så vore det ju väldigt bra om modellen kunde säga när den var säker och inte. Kanske är det t.ex så att när medel-ryckigheten är över 7 så kan man ganska säkert säga att en svag axel går av efter ca 1000 mil, men när ryckigheten är låg så är vi mer osäkra. Detta skulle kunna bero på att axeln då inte går av, men det finns ju en massa andra fel som kan uppstå som vi inte har bra sensorer för, så vi vet helt enkelt inte. På finspråk kallas detta heteroskedastisk (olika för olika indata) aleatorisk (vi saknar variabler/sensorer) osäkerhet.
Om modellen är olika säker för olika input så kan den, om den är tränad för det, svara med både vad den tror och hur säker den är, vilket kan hjälpa en människa som försöker ta ett beslut om service. Snyggt! Nu är vi väl färdiga? Nja.
Mer än bara ett osäkerhetsvärde
Hur uttrycker man egentligen osäkerhet? Ett vanligt sätt är standardavvikelse, σ. Om vår modell för en viss fråga anger σ=100 mil och våra fel är normalfördelade så betyder det att för detta svar så kommer 68% av resultaten ligga inom ±100 mil från prediktionen och 95% inom ±200 mil. Så fungerar standardavvikelse. Men felen är sällan normalfördelade. En vanlig anledning är t.ex som i detta exempel, när negativa resultat inte är rimliga. I statistik kallas det helt enkelt skevhet när osäkerheten är asymmetrisk. Ytterligare en parameter man kan prata om är kurtosis – hur sannolika är riktigt extrema utfall? Med andra ord, hur tjocka är mina svansar?
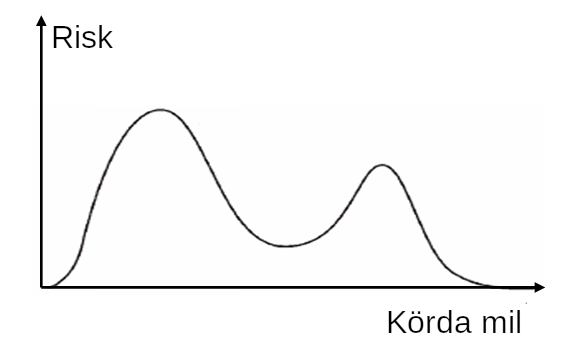
Allt detta skulle kunna vara intressant eller ointressant beroende på vad modellen ska användas till. Om modellens utfall ska visas för en människa, så är det nog väldigt ovanligt att denne kommer uppskatta ointiutiva siffror på kurtosis och skevhet. Då kan det vara bättre att helt enkelt rita ut hela distributionen, om din modell klarar att ge en helt fri täthetsfunktion som svar. För en viss medel-ryckighet, kanske modellen egentligen skulle vilja svara såhär:
Det är väldigt ovanligt med modeller som klarar att ge så detaljerade svar, men på Tenfifty har vi faktiskt minst en kund där allt hänger på att vi kan beräkna och visa sådana täthetsfunktioner, samt planera och simulera över dem.
Vi kan även se att vårt svar har två toppar. Detta kallas att den är bimodal. I vårt lastbilsfall kan det till exempel bero på att företaget kör primärt i två regioner, där den ena har ett mycket tuffare klimat. Om modellen inte får veta vilken region som lastbilen kör i så blir det ju väldigt konstigt om den måste ange ett medel mellan topparna – detta är anledningen till att ett enda värde ibland kan vara så missvisande. Då är det mycket bättre om modellen kan säga att “antingen så blir det fel ungefär då, eller då”. Återigen så är det för att vi saknar indata. Aleatorisk osäkerhet. Om denna insikt inte kan hjälpa till bättre beslut, så kan den åtminstone säga att det kanske är dags att samla in fler sorters data. Att en kolumn saknas i din databas.
Men nu är vi väl färdiga? Nja.
Epistemisk osäkerhet
Man kan naturligtvis gräva ned sig hur långt som helst kring risk och osäkerhet och vad som är viktigt skiljer från fall till fall, men det finns ytterligare en viktig osäkerhetskälla. Epistemisk osäkerhet. Vad händer om indata ligger utanför en region som modellen fått se i den insamlade datan? Eller i en region där det är glest med data? Om aleatorisk osäkerhet betyder att det saknas kolumner i din databas, så betyder epistemisk osäkerhet att det saknas rader.
Om det största värdet på medel-ryckighet som du någonsin sett är 23 och det plötsligt kommer en lastbil med medel-ryckighet på 60, vad tror du kommer hända? Hur säker är du? Detta är ett ganska filosofiskt ämne, men vad man kan säga i korthet är att vissa modeller försöker att ta med även denna typen av osäkerhet och för en mänsklig mottagare eller ett system så kan det vara väldigt viktigt att veta att anledningen till att jag är osäker är att jag helt enkelt aldrig har sett eller hört talas om en sånhär situation.
Sammanfattningsvis – en AI-modell är inte ett magiskt orakel som ger ett tal som du kan ta som en komplett sanning. Det kan ligga mycket komplexitet gömd bakom talet. Komplexitet som du kanske behöver veta.
Välj en AI-leverantör som vet när de inte vet.